Engineering Better Disaster Relief

Rhonda Righter. (Photo by Peg Skorpinski)
Scheduling problems, which involve searching for an optimal or near-optimal schedule for a set of tasks, are notoriously complex because simple searches are overwhelmed by their explosively vast number of possibilities. But with large-scale manufacturing and distribution operations, fractional improvements in scheduling can have large-scale impacts on the bottom line, which is why industrial engineers are routinely called upon to create customized sophisticated strategies for specific scheduling problems.
Now, Professor Rhonda Righter has applied industrial engineering–style analysis to a different type of scheduling problem: after a mass casualty event, such as a natural disaster, a wreck or an attack, how should a medical emergency response team allocate its attention to patients, in order to save the most lives?
Patients routinely wait for doctors, as the joke goes; that’s why they’re called “patients.” But after disasters, severely injured people may die for lack of prompt medical attention. This is when triage, prioritizing patients according to their injury severity, becomes important. “The military trains their doctors to think about these issues,” Righter says, “But on the civilian side, ER doctors don’t always know how to handle major triage.”
Righter (Ph.D.’86 IEOR) is professor and chair of UC Berkeley’s Department of Industrial Engineering and Operations Research. In a recent paper, she and her colleagues, Nilay Tanik Argon and Serhan Ziya from the University of North Carolina at Chapel Hill, noted that the relationship between disaster casualties and an emergency medical team resembles, in abstract terms, the relationship between a job queue and a server, with jobs quitting the queue if they aren’t served within a certain time. From this perspective, triage becomes a scheduling problem, and its optimal solution is the schedule that yields the fewest possible job timeouts.
To model this dynamic, Righter and her colleagues represented each patient with two numbers: how long they can survive without medical attention and how long their treatments require. When these two numbers are positively correlated, that is, when the most critical patients are also the quickest to treat, the optimal strategy is obvious: Treat the most critical patients first. But the more realistic, inverse relationship is more challenging. “Where it becomes interesting is when there’s a tradeoff,” Righter explains, “when the more critically injured patients require longer attention and the ones who can survive a longer wait could be taken care of relatively quickly.”

An industrial engineering–type approach to scheduling problems may help emergency responders allocate resources after a mass casualty event, such as a natural disaster or auto accident, according to a recent report by Berkeley’s Rhonda Righter and colleagues.
The researchers modeled patients as falling into these two groups. This allowed them to represent each treatment strategy as a two-dimensional, black and white graph, where the axes correspond to the numbers of patients in each group, and the points dictate which type of patient should be handled next. For example, if you had 13 critical/slow and 14 noncritical/fast patients remaining, you find the point (13, 14) on the graph. If it’s black, you treat a critical patient next, and if it’s white, you treat a noncritical patient. After that patient is taken care of, you find your new place on the graph to pick the next one.
Optimal schedules varied for different distributions of criticality and treatment times, but they shared a pattern: with limited casualties, you save more lives by treating the critical patients first, and with larger numbers, you do better starting with noncritical patients. “As the numbers pile up,” Righter explains, “it’s better to take care of the short-time patients first to get them out the door.”
Righter and her colleagues don’t expect overwhelmed medical teams to start using tracking systems and graphs to optimize triage, but their findings do point to a realistic lifesaving approach: develop simple and easily remembered triage rules that at least resemble the optimal strategies, and teach them to the teams working on the ground. In computer science, such rules are called heuristics. “It would be hard to implement the gory details of optimal scheduling,” Righter says, “But it’s good for people to have general heuristics in mind.”
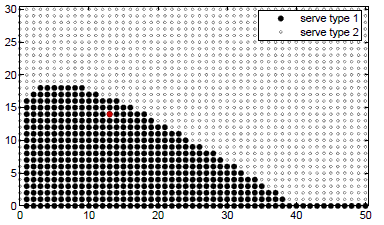
In this graphic representation of the optimal heuristic strategy, the x-axis shows the number of critical/slow patients waiting and the y-axis the number of noncritical/fast patients. The red dot here, for example, corresponds to 13 critical/slow and 14 noncritical/fast patients remaining. Light dots signify that a noncritical patient should be treated next (then move down on graph), and dark dots signify that a critical patient should be treated next (then move to the left on graph). (Photo by The Researchers.)
The researchers developed two such heuristics. One, which looks like a triangle on the graph, prescribes working on noncritical/fast patients until the total number of patients waiting falls below some threshold, say 40. The other heuristic, which looks rectangular, prescribes treating noncritical injuries until the number in either group drops below a threshold, say 20. Both rules require only that team members remember a single number and have an awareness of whether the current backlog of casualties is above that number.
Righter and her colleagues evaluated the heuristics’ performance in simulation against the optimal strategy, along with a heuristic from a 2004 paper by Scottish researchers and the “time-critical first” strategy commonly practiced by doctors without training in triage. When patients are dying fast, the triangular heuristic usually saved the most lives. In a less dire situation, the rectangular strategy gets the edge. In most scenarios, both strategies outperformed the 2004 heuristic. And in all cases, they had better average outcomes than the time-critical-first strategy that medical practitioners naturally tend to follow as they gravitate toward the patient who currently needs them the most.
“When doctors see a patient, they think, ‘How can I do the best thing for this individual?'” Righter explains. “The temptation is to err on the side of caring too much for the person in front of you. But under triage, you save more lives with a utilitarian mindset that backs up and asks, ‘How can I do the greatest good for the greatest number of people?'”
Righter et al paper: Argon, N. T., S. Ziya, and R. Righter, “Scheduling impatient jobs in a clearing system with insights on patient triage in mass-casualty incidents,” Probability in the Engineering and Informational Sciences 22 (2008), 301-332.
